题目链接：The 2018 ACM-ICPC Asia Qingdao Regional Contest, Online - Problem I

感谢东南大学的 CoupDeGrace 同学提供本题题解。

# 题目描述

As we know, DreamGrid is a master of planning algorithm. Recently, a new type of autonomous car appears in Gridland. With the shape of a circle, the car can move in any direction. Being interested in this car, DreamGrid decides to design a specific path planning algorithm for it. Here is the first case he wants to solve.

Consider two cars on the two-dimensional plane with the same radius of $r$. We now want to move the center of the first car from $(0, 0)$ to $(d, 0)$, where $d$ is positive. The second car, starting its move with its center located at $(2r, 0)$, can be considered as an obstacle moving towards the positive direction of the x-axis with a constant speed of $v$. Luckily, after installing a new engine, the first car can move twice as fast as the obstacle car, which means the maximum speed of the first car can be $2v$.

DreamGrid wants to know the shortest time needed to move the first car to the end point without colliding with the second car. That is to say, before arriving at the end point, the circle representing the first car can’t intersect with (but can be tangent to) the circle representing the second car.

As DreamGrid is too busy, you are asked to solve this simple problem for him. Of course, if you successfully solve this problem, you will get a brand-new autonomous car in the Gridland!

# Input

There are multiple test cases. The first line of the input is an integer $T$($1 \le T \le 1000$), indicating the number of test cases. For each test case:

The only line contains three real numbers $v, r, d$($1 \le v, r \le 10, 1 \le d \le 100$) with at most two digits after the decimal point, indicating the radius of the car, the speed of the obstacle car and the distance between the start point and end point.

# Output

For each test case output one line, indicating the shortest time for the first car to arrive the end point without colliding with the second car. Your answer will be considered correct if and only if the absolute error or relative error of your answer is less than $10 ^ {-6}$.

# Sample Input

1
2.00 3 30.0

# Sample Output

8.310579933902352

# 题目大意

有两个半径相同(为$r$)的圆，记为$A$, $B$。初始，$A$圆心位于$(0, 0)$, B圆心位于$(2r, 0)$。$B$圆以速度$v$向$x$轴正方向做匀速直线运动，$A$圆由玩家操控，可以随时改变方向和速度(最高速度为$2v$)，要求在任何时刻两圆不能相交(可以相切)，询问$A$圆到达点$(d, 0)$的最短时间。

# 思路

首先，很容易想到，让$A$圆紧跟着$B$圆做速度为$v$的匀速直线运动一定是合法的，用时为$\frac{d}{v}$，这是答案的上界。 比较自然的，我们想到可以让$A$圆保持与$B$圆相切，从$B$圆上方滚过去，滚动到某一个角度以后，再直线运动到终点。再简化一下，只保留$A$, $B$两圆的圆心，仍然记为$A$, $B$。

第一部分的运动轨迹：假设过去了时间$t$

$B$点方程很好写：

$$ \begin{cases} x = 2 r + v t \\ y = 0 \end{cases} $$

$A$点的有点烦，运动分解为紧随$B$点的速率为$v$的匀速直线运动以及以$B$点为圆心，半径为$2r$的变速率圆周运动。

记$\alpha$为$AB$连线与$x$轴负方向的夹角，定义域为$[0,\pi]$ $A$点：

$$ \begin{cases} x = 2 r + v t - 2 r \cos \alpha \\ y = 2r \sin \alpha \end{cases} $$

似乎有点眼熟啊，这玩意不是个摆线吗。嘤嘤嘤，不想做曲线积分算摆线长度，换个思路用$\alpha$表示一下时间$t$。 如图，假设某一时刻，$AB$连线与$x$轴负方向的夹角为$\beta$，此时$A$, $B$相对运动关系如下，$V_t$是$A$在圆周上的切向速度，$V_x$和$V_y$是$V_t$的分解。

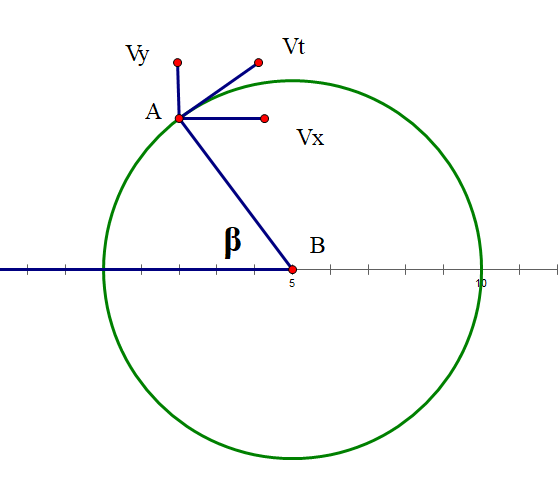
列个方程组

$$ \begin{cases} V_x = V t \sin \beta \\ V_y = V t \cos \beta \\ (V_x + v) ^ 2 + V_y ^ 2 = (2 v) ^ 2 \end{cases} $$

解得 $V_t = v(\sqrt{\sin^2 \beta + 3} - \sin \beta)$

所以

$$ t = \int_{0}^{\alpha} \frac{2 r}{v(\sqrt{\sin^2 \beta + 3} - \sin \beta)} d\beta $$

这个积分没有初等解，我们可以掏出 Wavator 的simpson板子。- 所以第一部分的方程推完了，嘤嘤嘤。

第二部分就比较easy了，用时非常显然，即为$\frac{\sqrt{(d - x) ^ 2 + y ^ 2}}{2 v}$。下面的关键就在于确定两部分之间的分界点$\alpha$。显然，分界点$\alpha$必然在$[\pi/2, \pi]$之间，是摆线下降段的某个位置，很容易想到可以二分去做。 如何判断某一个$\alpha$是否可行？我们可以在运动模式变化瞬间，取一个微元$Δt$判断一下$AB$之间的距离是否会变小。设$(x, y)$为该时刻$A$点坐标：

$$ \beta = \arctan{(\frac{y}{d - x})} $$

$$ \Delta = (x - (2 r + v t)) \cdot (2 v \cos \beta - v) - (y - 0) \cdot 2 v \cos \beta $$

判别式$\Delta$不为负时$\alpha$可行（这个就不证明了嘤嘤嘤）

最终答案即为$\frac{\sqrt{(d - x) ^ 2 + y ^ 2}}{2 v} + t$

要注意的是，如果摆线一个周期的横坐标长度已经超过了$d$，直接输出$\frac{d}{v}$。

缅怀一下曾经的PHO打铁时光。

# 代码

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61

#include<bits/stdc++.h>
using namespace std;
long long i,j,k,s,t,T,n,m,pp;
double l,r,d,R,v,mid,eps=1e-9,ans,temp,pi,x,y,vx,vy,xx,yy,halfpi,beta,maxn;
double f(double x)
{
    double temp=sin(x);
    return 1.0/(sqrt(temp*temp+3)-temp);
}
double Simpson(double l, double r)
{
    double m = (l + r) / 2;
    return (f(l) + 4 * f(m) + f(r)) * (r - l) / 6;
}
double cal(double l, double r, double res,double eps)
{
    double m = (l + r) / 2;
    double L = Simpson(l, m), R = Simpson(m, r);
    if (abs(L + R - res) <= 15 * eps) return L + R + (L + R - res) / 15;
    else return cal(l, m, L, eps / 2) + cal(m, r, R, eps / 2);
}
int main()
{
    halfpi=acos(0.0);
    pi=acos(-1.0);
    scanf("%lld",&T);
    maxn=2*(cal(0, pi, Simpson(0, pi),eps)+2);
    while (T--)
    {
        scanf("%lf%lf%lf",&v,&R,&d);
        ans=d/v;
        if (d <= maxn * R)
        {
            printf("%.12f\n", ans);
            continue;
        }
        l=halfpi;r=pi;
        while ((r-l)>eps)
        {
            mid=(l+r)*0.5;
            temp = cal(0, mid, Simpson(0, mid),eps);
            x= 2*R*(temp+1+sin(mid-halfpi));
            yy=y= 2*R*cos(mid-halfpi);
            xx=2*R*sin(mid-halfpi);
            beta=atan(y/(d-x));
            vx=2*cos(beta)-1;
            vy=2*sin(beta);
            vx=vx*sin(mid-halfpi);
            vy=vy*cos(mid-halfpi);
            if (vx>vy||fabs(vx-vy)<=eps)
            {
                r=mid;
                temp=temp*2*R/v;
                temp=temp+sqrt(y*y+(d-x)*(d-x))/(2*v);
                if (temp<ans) ans=temp;
            }
            else l=mid;
        }
        printf("%.12f\n",ans);
    }
}